1. Numeri complessi. Risolvere la seguente equazione nel campo complesso:
Rappresentare sul piano di Gauss le quattro soluzioni trovate,
indicandole con le lettere A, B, C, D. Calcolare l'area del quadrilatero
ABCD.
|
Si pone z2 = t e si
trovano de due radici dell'equazione di 2° grado in t. Di ciascuna di queste si estrae la radice quadrata (COMPLESSA!) e si trovano le quattro soluzioni dell'equazione di 4° grado. Il quadrilatero individuato nel piano di Gauss, dai quattro punti soluzione, è un rettangolo di lati noti inscritto in una circonferenza di raggio 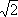
|
2. Studio di funzione. Tracciare il grafico della seguente funzione:
e calcolare l'area della regione di piano sotto il grafico della f(x)
a partire dal punto di ascissa ![]()
Lo studio di funzione non presenta alcuna difficoltà. Ha l'asse delle
ascisse come asintoto orizzontale destro, un massimo nel punto di ascissa
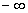 la funzione tende a
la funzione tende a 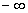 . .L'area sotto il grafico della funzione si ottiene calcolando un integrale generalizzato da 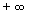 .
L'integrale è convergente. .
L'integrale è convergente.
|
3. Serie. Studiare la convergenza semplice ed assoluta della seguente
serie ( ![]() ma
ma
![]() ).
Calcolare la somma della serie quando x = 1999.
).
Calcolare la somma della serie quando x = 1999.
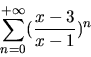
Si tratta di una serie geometrica di ragione 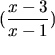 . .È convergente (assolutamente e semplicemente) per 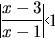 cioè per x > 2.
cioè per x > 2.Per x = 2 diventa serie indeterminata (OSCILLANTE) 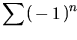 . .Per x = 1999 la serie converge e la sua somma è 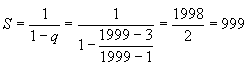
|
4. Integrali. Calcolare il seguente integrale indefinito:
|
L'integrale si può calcolare in diversi modi equivalenti. Ad esempio: - con sostituzione ponendo 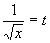 e poi per parti; e poi per parti;- prima per parti considerando 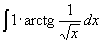 e poi per
sostituzione. e poi per
sostituzione.
|