Cognome, nome e Corso di Laurea:
...........................................................Matricola:..............
1. Numeri complessi. Risolvere la seguente equazione nel campo complesso:
2. Studio di funzione. Tracciare il grafico
della seguente funzione:
e calcolare l'area della regione di piano sotto il grafico della f(x) a partire dal punto di ascissa ![]()
3. Serie. Studiare la convergenza semplice ed assoluta della seguente serie (
![]() ma
ma ![]() ). Calcolare la somma della serie quando x = 1999.
). Calcolare la somma della serie quando x = 1999.
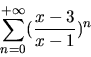
4. Integrali. Calcolare il seguente integrale indefinito: