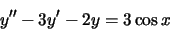
1. Equazioni differenziali. Risolvere il seguente Problema di Cauchy
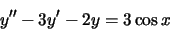
con le condizioni iniziali
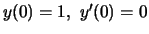 .
.
|
L'equazione del II ordine non presenta alcuna difficoltà: si trova prima
la soluzione generale dell'equazione omogenea associata mediante la ricerca delle radici del suo polinomio caratteristico 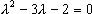 . .Poi si ricerca una soluzione particolare dell'equazione completa tenendo conto che questa potrà provenire da una combinazione lineare del tipo: Infine si impongono le condizioni iniziali. |
2. Studio di funzione. Tracciare il grafico della seguente funzione:
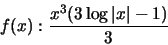
e calcolare l'area della regione di piano sotto il grafico della f(x) tra i punti di ascissa
![]() e 1
e 1
|
La funzione è dispari, per cui è sufficiente studiare il suo
comportamento solo su metà asse reale Possiede un minimo ed un massimo relativi nei rispettivi punti di ascissa Nel punto di ascissa La funzione non ha asintoti. |
3. Serie. Studiare la convergenza semplice ed assoluta della seguente
serie (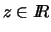 ).
).
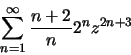
La serie si studia preliminarmente considerando il valore assoluto (assoluta
convergenza). In tal modo possiamo applicare un opportuno criterio di convergenza,
ad esempio quello del rapporto, che fornisce come risultato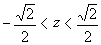 Agli estremi di tale intervallo la serie non converge (manca ad esempio la condizione necessaria). |
4. Integrali. Calcolare il seguente integrale indefinito:
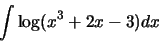
|
L'integrale si può risolvere per parti considerando come al solito il
prodotto
L'integrale che ne deriva è quello di una funzione razionale che può essere scomposta in somma di frazioni più semplici. |