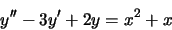
1. Equazioni differenziali. Risolvere il seguente Problema di Cauchy
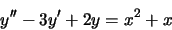
con le condizioni iniziali
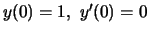 .
.
|
Il secondo membro dell'equazione è un polinomio di secondo grado, quindi
una soluzione particolare potrà essere del tipo
Per la soluzione dell'omogenea associata è sufficiente trovare le 2 radici reali e distinte del polinomio caratteristico 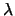 2 - 3 2 - 3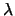 + 2. + 2. |
2. Studio di funzione. Tracciare il grafico della seguente funzione:
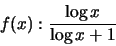
|
La funzione presenta un asintoto verticale in
È sempre crescente ed ha un flesso nel punto di ascissa |
3. Successione. Al variare del parametro reale
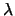 determinare per quali valori di tale parametro
la successione è limitata, convergente, divergente.
determinare per quali valori di tale parametro
la successione è limitata, convergente, divergente.
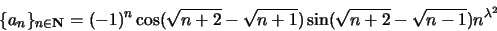 .
.
La successione, dopo opportuna razionalizzazione degli argomenti del seno e del
coseno, è assimilabile a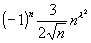 che si ottiene osservando che il coseno tende a 1 mentre il seno può essere approssimato col suo argomento. A questo punto l'indice "critico" è 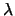 2 - ½ 2 - ½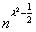 . .Per 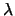 = ± = ± 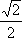 per 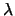 < - < - 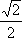 e e 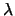 > > 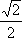 per 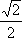 < < 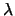 < < 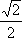 |
4. Integrali. Calcolare il seguente integrale indefinito:
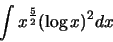
|
L'integrale si risolve con due applicazioni successive del metodo di integrazione
per parti. La scelta migliore per la ricerca della primitiva è banalmente, la funzione 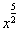
|